El mes passat vaig exposar fenòmens de l’anomenada Mecànica Quàntica (o Teoria Quàntica) que sorprenen els físics quan estudien el món de les partícules atòmiques, i que semblen màgics. Curiosament, quan el meu article estava a punt de sortir a Emporion, el Magazine dominical de La Vanguardia del dia 26 de setembre ens donava la bona notícia que un físic fill de Manresa, Ignasi Cirac, de 30 anys, director de l’Institut Max Planck d’Òptica Quàntica, a Alemanya, és un dels màxims aspirants a obtenir el premi Nobel de Física. Cirac és un dels cervells privilegiats que estudia les grans possibilitats que obre el món de la Teoria Quàntica, i segons explicava el Magazine, està projectant una nova espècie d’ordinadors, els ordinadors quàntics, que utilitzaran les propietats màgiques del món subatòmic, on les partícules poden ser a llocs diferents al mateix temps, o poden interectuar entre elles encara que les separin centenars de quilòmetres. I hi llegíem que Cirac també està ajudant els investigadors de l’Institut de Ciències Fotòniques de Catalunya, que –com vaig dir el mes passat- ara estan estudiant l’aplicació de la Teoria Quàntica a la medicina, i concretament (la notícia era a La Vanguardia del 25 de juliol passat), investiguen si els virus, com les partícules atòmiques, també poden ser a diversos llocs al mateix temps,… impressionant!
Abans d’exposar le teoria que es proposa per explicar tots aquests fenòmens i experiments, convé que parlem un moment d’atzar i de probabilitat. Tots tenim experiència de com influeix l’atzar a les nostres vides. La nostra mateixa vida és fruit de l’atzar, de què un espermatozou d’entre milions, per una sèrie de circumstàncies afortunades, arribi a fecundar un òvul. I el concepte d’atzar ens mena de seguida a un altre concepte: el de probabilitat. Si tirem moltes vegades una moneda a cara o creu, sabem que a la llarga s’equilibraran les vegades que surt una o altra, i diem que la probabilitat de sortir cara (o creu) és d’un 50%. Si tirem un dau que no sigui trucat, la probabilitat que surti 6 és d’un 1/6, cadascuna de les 6 cares té la mateixa probabilitat. I després de sortir un 6, altre cop totes les cares tenen la mateixa probabilitat de 1/6. Però sabem que si ha sortit 6 molts cops seguits, a la llarga han d’anar sortint les altres cares. Com ho “sap” el dau que ha d’anar equilibrant el joc i que no ha de sortir sempre el 6?
Apliquem-ho ara a les partícules subatòmiques (protons, electrons, etc). Quan una partícula llançada des d’un punt arriba a un altre punt, pot haver passat per infinitat de camins, però per uns amb una gran probabilitat, per altres amb una escassíssima probabiitat. Com diu Stephen Hawking, el famós físic, per posar un exemple: “tots els equips que competeixen al Mundial de futbol tenen una o altra probabilitat de guanyar-lo, també Burundi, encara que en aquest cas la probabilitat és baixíssima”. (Però de vegades aquesta probabilitat es dóna per una sèrie de circumstàncies totalment atzaroses, m’entendran bé els que hagin vist la pel·lícula “Slumdog millionaire”, aquell nen indi que encerta per una sèrie de circumstàncies excepcionals totes les preguntes d’un concurs de televisió).
Així doncs, basant-se en el càlcul de probabilitats, la teoria que s’ha proposat per explicar els fenòmens quàntics és la següent:
- En primer lloc es considera que en el món subatòmic els fotons, els electrons, totes les partícules, siguin d’energia o de matèria, poden seguir tots els camins per anar d’un lloc a un altre, tots els camins són possibles al mateix temps.
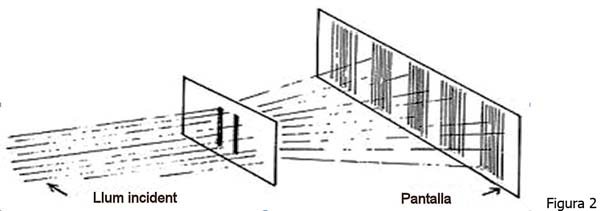
- Per tant, un mateix fotó, o un mateix electró, o qualsevol partícula, podria ser, amb una certa probabilitat repartida, a tots els camins alhora, amb més probabilitat en uns camins que en altres, i per això (vegeu Figura 1) la partícula “sap” quan hi ha una escletxa o quan hi ha dues escletxes, i “què ha de fer” en cada cas.
Segons el gran físic teòric Richard Feynman, el camí de la partícula entre A i B (vegeu Figura 2) seria la suma de les probabilitats de tots els llocs on la partícula podria ser al mateix temps en cada moment!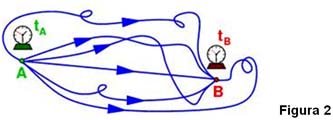
Albert Einstein mai no va acceptar la Mecànica Quàntica, tot i que havia ajudat a crea-la, i deia que “Déu no juga amb daus”. Lo admirable és que una quantitat enorme d’experiments han demostrat que Einstein estava equivocat, que “Déu certament juga amb daus”, que la teoria, encara que no l’entenguem, és encertada, i que fins ara cap experiment no l’ha rebatuda.
És per això que Ignasi Cirac i els investigadors de l’Institut de Ciències Fotòniques de Catalunya intenten ara aplicar la Teoria Quàntica a la medicina estudiant si un virus pot ser a dos llocs alhora. Els virus són prou petits per poder-se comparar amb protons o electrons? On és el límit entre lo microscòpic i lo ultramicroscòpic?
- Em cal afegir un altre element essencial de la mecànica quàntica, també misteriós, si voleu. És el principi d’incertesa de Heisenberg, que diu que no és possible saber exactament el lloc on és una partícula i al mateix temps la seva velocitat, que si coneixem una de les dues dades, desconeixem l’altra. (Com si al futbol un porter pogués veure la pilota que ha xutat un davanter, però no pogués saber cap on irà i amb quina força, i si li diguéssin la velocitat no pogués saber on és la pilota).
He de repetir un cop més que no ens ha d’espantar no entendre bé tots aquests conceptes, que allò que intento amb aquests articles només és que ens fem una idea de per on ha anat la ciència del segle XX, i de cap a on ens porta actualment. I repeteixo també que tot aquest edifici intel·lectual està aixecat sobre uns fonaments matemàtics precisos, i que ha estat comprovat amb nombrosíssimes experiències pràctiques.





